Search
castle

ComputerVision▼

Loss function

image.png

  • loss function, objective function, cost function
  • 모델 성능을 예측하는 지표
  • 모델의 예측값(output)과 실제 값(Target Value)과의 차이
    • Object detection - target value대신 ground truth 용어 사용
  • 최적의 weight값을 조절하는데 사용(loss function의 값이 0과 가깝게 되는 것이 목표)
  • 출력층의 activation function에 따라 loss function의 종류 결정

출처: [https://modulabs.co.kr/blog/loss-function-machinelearning](https://modulabs.co.kr/blog/loss-function-machinelearning)

출처: https://modulabs.co.kr/blog/loss-function-machinelearning

  • softmax에서의 loss function

Back propagation

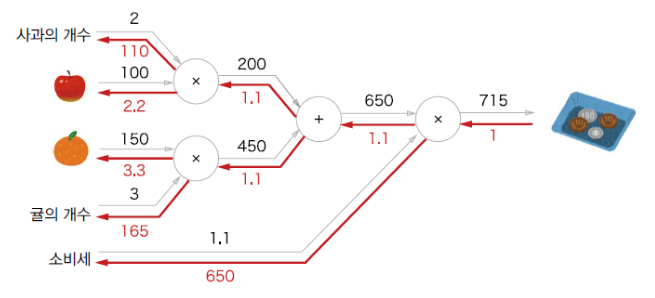
image.png

  • 정답(target value)과 모델의 결과(score) 오차 계산
  • 흔히 deep learning의 ”학습”이라고 불르는 과정
  • 오차의 크기가 적어지는 방향으로 가중치(weights) 갱신
  • 결과적으로 모델의 결과(score)가 정답(target value)와 근접하도록 weight를 수정하는 과정

SGD

GD(Gradient Descent)

image.png

  • 산을 내려갈 때 아래 방향 경사(기울기)를 타고 내려가는 것과 동일한 방식(Gradient Descent)
  • 기울기하면 생각나는 그것
  • 미분 방정식 사용
  • \[W(t+1) = W_t - \frac{\partial \text{오차}}{\partial W}\]

출처: [https://velog.io/@nochesita/딥러닝-오차역전파-Backpropagation](https://velog.io/@nochesita/%EB%94%A5%EB%9F%AC%EB%8B%9D-%EC%98%A4%EC%B0%A8%EC%97%AD%EC%A0%84%ED%8C%8C-Backpropagation)

출처: https://velog.io/@nochesita/딥러닝-오차역전파-Backpropagation

  • 이걸 어케 설명해

SGD(Stochastic + Gradient Descent)

출처: [https://www.analyticsvidhya.com/blog/2021/03/variants-of-gradient-descent-algorithm/](https://www.analyticsvidhya.com/blog/2021/03/variants-of-gradient-descent-algorithm/)

출처: https://www.analyticsvidhya.com/blog/2021/03/variants-of-gradient-descent-algorithm/

  • input layer의 데이터의 수가 많을 경우 Gradient Descent의 연산량이 급격히 증가
  • 연산량을 줄이기 위해 데이터를 나눠서 학습
  • 하나의 dataset을 학습한 후 평균을 사용
  • Mini-Batch GD
    • Batch Size = 데이터 묶음 개수
    • 위의 예시에서는 5개의 데이터 중 2개씩 학습 실행
    • 일반적으로 Batch Size = 32/64/128(\(2^n\)) 사용
    • SGD(Batch Size == 1)는 거의 안쓰나 대부분의 경우 Mini-Batch GD를 의미함
    • Stochastic의 의미가 확률론적이라는데 왜 이렇게 작명했는지는 모름
  • 연산량 말고도 실행 횟수의 의미도 있음
  • 실행 횟수가 많다 → Back propagation이 많다 → 학습을 더 많이 수행한다
    • 하지만 deep learning에서 중요한 Batch Normal의 영향이 줄어드는 단점이 존재한다
    • Batch Size의 경우 크게 신경쓰지 말고 CPU가 버티는 범위에서 크게 설정(하라고 교수가 말했음)

Optimization

SGD의 문제점

  1. 학습률이 다름
  2. local & global minimum, saddle point

image.png

  • Mini-Batch는 dataset을 나누어 사용
    • Batch들의 데이터 차이 → 학습 iteration마다 학습률이 다름

image.png

출처: [https://heeya-stupidbutstudying.tistory.com/entry/ML-신경망에서의-Optimizer-역할과-종류](https://heeya-stupidbutstudying.tistory.com/entry/ML-%EC%8B%A0%EA%B2%BD%EB%A7%9D%EC%97%90%EC%84%9C%EC%9D%98-Optimizer-%EC%97%AD%ED%95%A0%EA%B3%BC-%EC%A2%85%EB%A5%98)

출처: https://heeya-stupidbutstudying.tistory.com/entry/ML-신경망에서의-Optimizer-역할과-종류

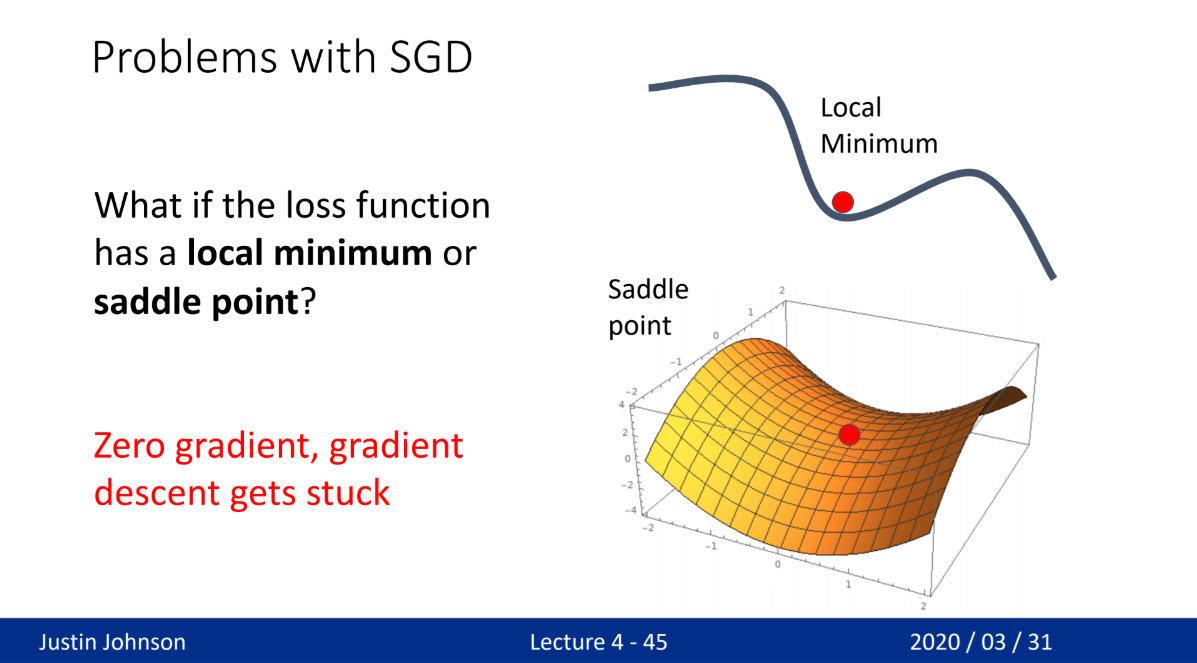
  • local & global minimum, saddle point
  • 오차의 기울기에 따라 학습 → 기울기가 0 지점에서는 학습이 안됨(saddle point)
  • 기울기가 너무 클 경우 최적 해를 지나치거나, 작을경우 최적해가 아닌 다른 해에서 학습이 끝날 수 있음

SGD의 변형

출처: [https://www.slideshare.net/yongho/ss-79607172](https://www.slideshare.net/yongho/ss-79607172)

출처: https://www.slideshare.net/yongho/ss-79607172

  • Momentum, RMSProp, Adam - 가장 많이 사용

image.png

image.png

  1. Momentum
    • 움직이는(학습) 방향으로 관성을 적용
    • 기존에 이동하던 방향을 다음 학습에 적용하여 방향성을 유지하는 방식
    • Nestrerov Momentum: Momentum보다 좀 더 좋은 방식
  2. RMSProp
    • 각 가중치의 학습률을 개별적으로 조정 → 학습이 빠른 방향은 학습률 감소, 느린 방향은 유지
    • 이를 통해 가파른 방향(steep direction)에서는 진동을 줄이고, 완만한 방향(shallow direction)에서는 더 빠르게 이동 가능
    • 최적점 주변에서 안정적인 수렴 가능
  3. Adam (Adaptive Moment Estimation)
    • Momentum + RMSProp의 장점을 합친 최적화 알고리즘
    • 모르겠으면 Adam 쓰면 된다

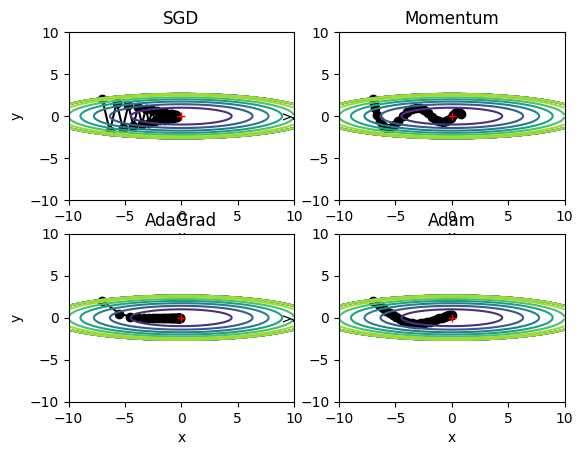
SGD 비교

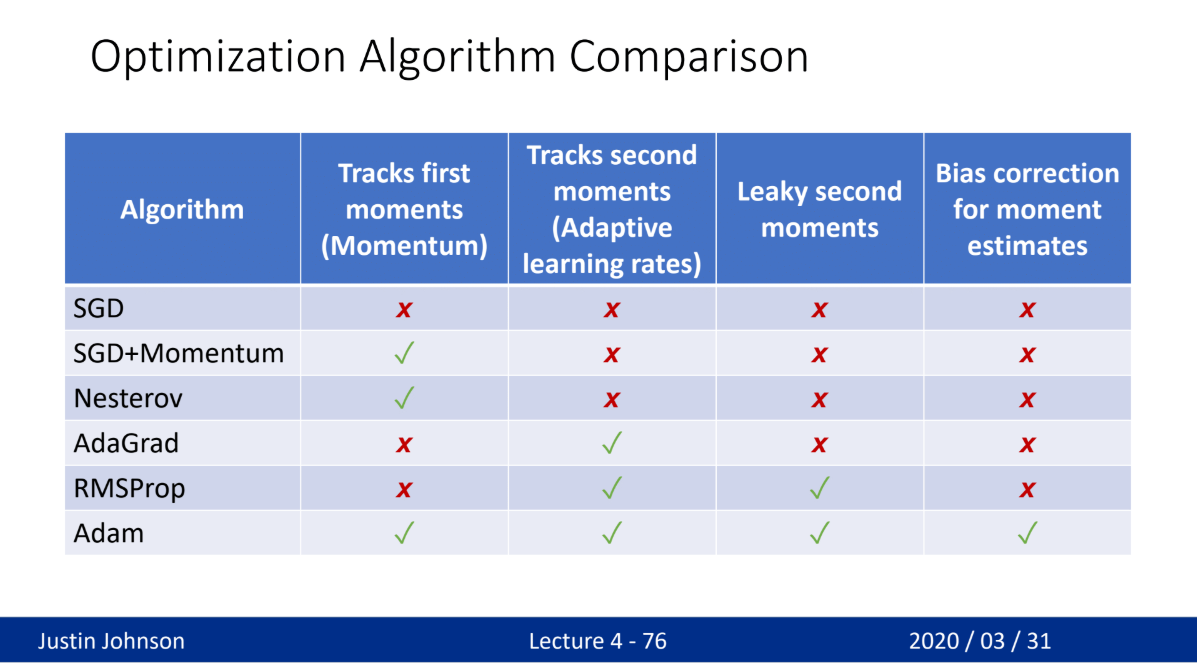
image.png

  • Adam은 신이다

image.png

출처: [https://www.researchgate.net/figure/Confusion-matrixes-a-RMSprop-optimizer-b-SGD-optimizer-c-Adam-optimizer_fig1_361744456](https://www.researchgate.net/figure/Confusion-matrixes-a-RMSprop-optimizer-b-SGD-optimizer-c-Adam-optimizer_fig1_361744456)

출처: https://www.researchgate.net/figure/Confusion-matrixes-a-RMSprop-optimizer-b-SGD-optimizer-c-Adam-optimizer_fig1_361744456

x
left
right

C

Contents

© Copyright 2025 jhj